Box2D C++ tutorials - Ray casting
Last edited: July 14 2013
Chinese version ->
中文
Ray casting
Ray casting is often used to find out what objects are in a certain part
of the world. A ray is just a straight line, and we can use a function provided
by Box2D to check if the line crosses a
fixture. We can also find out
what the normal is at the point the line hits the fixture.
Here is the function I'm talking about, which returns true if the ray hits the
fixture. Notice it's a member of the b2Fixture class,
which means we'll first need to have one of those to cast a ray against.
1
| bool b2Fixture::RayCast(b2RayCastOutput* output, const b2RayCastInput& input); |
Now what are these input and output parameters. Well, straight from the source code
here is what a b2RayCastInput contains:
1
2
3
4
5
6
| // Ray-cast input data. The ray extends from p1 to p1 + maxFraction * (p2 - p1).
struct b2RayCastInput
{
b2Vec2 p1, p2;
float32 maxFraction;
}; |
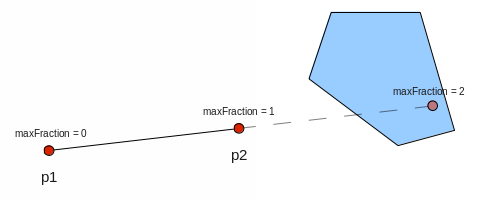
The points p1 and p2 are used to define a direction for the ray, and the
maxFraction specifies how far along the ray should be checked for an intersection.
The following image may make this clearer. A maxFraction of 1 simply means the segment
from p1 to p2, which in this case would not intersect the shape, but a maxFraction of 2 would.
And here is what a b2RayCastOutput contains:
1
2
3
4
5
6
7
| // Ray-cast output data. The ray hits at p1 + fraction * (p2 - p1), where p1 and p2
// come from b2RayCastInput.
struct b2RayCastOutput
{
b2Vec2 normal;
float32 fraction;
}; |
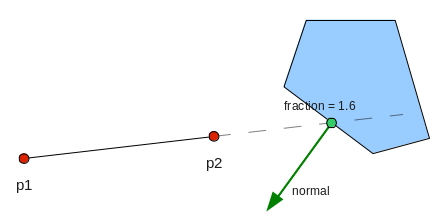
If the ray does intersect the shape, b2Fixture::RayCast will return true and we can
look in the output struct to find the actual fraction of the intersect point,
and the normal of the fixture 'surface' at that point:
Example
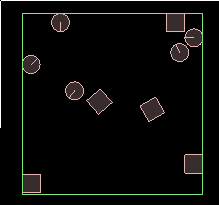
To try out this very handy function, let's set up a scene with a fenced area and
some shapes floating inside in a zero-gravity environment. By now you should be
getting used to this one, so we'll make the walls as edges instead of boxes just
to spice things up.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| FooTest() {
//a static body
b2BodyDef myBodyDef;
myBodyDef.type = b2_staticBody;
myBodyDef.position.Set(0, 0);
b2Body* staticBody = m_world->CreateBody(&myBodyDef);
//shape definition
b2PolygonShape polygonShape;
//fixture definition
b2FixtureDef myFixtureDef;
myFixtureDef.shape = &polygonShape;
//add four walls to the static body
b2Vec2 bl(-20, 0);
b2Vec2 br( 20, 0);
b2Vec2 tl(-20,40);
b2Vec2 tr( 20,40);
polygonShape.SetAsEdge( bl, br ); //ground
staticBody->CreateFixture(&myFixtureDef);
polygonShape.SetAsEdge( tl, tr);//ceiling
staticBody->CreateFixture(&myFixtureDef);
polygonShape.SetAsEdge( bl, tl );//left wall
staticBody->CreateFixture(&myFixtureDef);
polygonShape.SetAsEdge( br, tr );//right wall
staticBody->CreateFixture(&myFixtureDef);
myBodyDef.type = b2_dynamicBody;
myBodyDef.position.Set(0,20);
polygonShape.SetAsBox(2,2);
myFixtureDef.density = 1;
for (int i = 0; i < 5; i++)
m_world->CreateBody(&myBodyDef)->CreateFixture(&myFixtureDef);
//circles
b2CircleShape circleShape;
circleShape.m_radius = 2;
myFixtureDef.shape = &circleShape;
for (int i = 0; i < 5; i++)
m_world->CreateBody(&myBodyDef)->CreateFixture(&myFixtureDef);
//turn gravity off
m_world->SetGravity( b2Vec2(0,0) );
} |
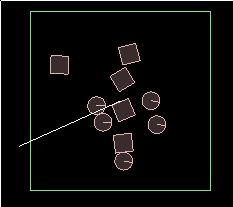
Now we need a ray to cast against these shapes. Let's make a ray starting
from the center of the screen and going outward, and rotating slowly around.
The only state we need to keep for this is the current angle, so instead of
making a special class for it, we'll just keep a variable at global scope.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| //at global scope
float currentRayAngle = 0;
//in Step() function
currentRayAngle += 360 / 20.0 / 60.0 * DEGTORAD; //one revolution every 20 seconds
//calculate points of ray
float rayLength = 25; //long enough to hit the walls
b2Vec2 p1( 0, 20 ); //center of scene
b2Vec2 p2 = p1 + rayLength * b2Vec2( sinf(currentRayAngle), cosf(currentRayAngle) );
//draw a line
glColor3f(1,1,1); //white
glBegin(GL_LINES);
glVertex2f( p1.x, p1.y );
glVertex2f( p2.x, p2.y );
glEnd(); |
You should now see a white line circling the scene. Now we just need to use the
RayCast function to get the distance to the closest intersected shape, and
draw the line at that length. We will check every fixture of every shape, which is
not the best way to do this, but will do as an example (see the
world querying topic
for a more efficient method). It also means we can take
a look at how you can iterate over the contents of the world:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| //in Step() function, continuing on from section above
//set up input
b2RayCastInput input;
input.p1 = p1;
input.p2 = p2;
input.maxFraction = 1;
//check every fixture of every body to find closest
float closestFraction = 1; //start with end of line as p2
b2Vec2 intersectionNormal(0,0);
for (b2Body* b = m_world->GetBodyList(); b; b = b->GetNext()) {
for (b2Fixture* f = b->GetFixtureList(); f; f = f->GetNext()) {
b2RayCastOutput output;
if ( ! f->RayCast( &output, input ) )
continue;
if ( output.fraction < closestFraction ) {
closestFraction = output.fraction;
intersectionNormal = output.normal;
}
}
}
b2Vec2 intersectionPoint = p1 + closestFraction * (p2 - p1);
//draw a line
glColor3f(1,1,1); //white
glBegin(GL_LINES);
glVertex2f( p1.x, p1.y );
glVertex2f( intersectionPoint.x, intersectionPoint.y );
glEnd();
//draw a point at the intersection point
glPointSize(5);
glBegin(GL_POINTS);
glVertex2f( intersectionPoint.x, intersectionPoint.y );
glEnd(); |
You might notice that now we are drawing two lines on top of each other... for clarity, delete the first one
and you should get this result:
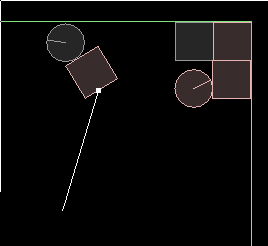
Well that's about all there is to finding the intersection point. We can use the normal in the
output struct for some interesting stuff though, so let's try it out. First, we'll simply render
the normal to see what it looks like:
1
2
3
4
5
6
7
| //draw intersection normal
b2Vec2 normalEnd = intersectionPoint + intersectionNormal;
glColor3f(0,1,0); //green
glBegin(GL_LINES);
glVertex2f( intersectionPoint.x, intersectionPoint.y );
glVertex2f( normalEnd.x, normalEnd.y );
glEnd(); |
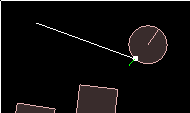
And for a grand finale, we can put the raycasting code into its own function and
call it recursively to reflect the ray off the intersected fixtures until it runs out. This is not
really anything to do with Box2D, I just think it's neat :)
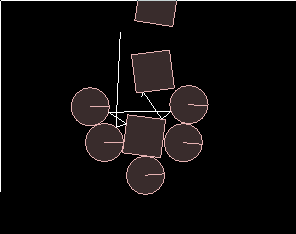
Here is the code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| //new function for FooTest class
void drawReflectedRay( b2Vec2 p1, b2Vec2 p2 )
{
//set up input
b2RayCastInput input;
input.p1 = p1;
input.p2 = p2;
input.maxFraction = 1;
//check every fixture of every body to find closest
float closestFraction = 1; //start with end of line as p2
b2Vec2 intersectionNormal(0,0);
for (b2Body* b = m_world->GetBodyList(); b; b = b->GetNext()) {
for (b2Fixture* f = b->GetFixtureList(); f; f = f->GetNext()) {
b2RayCastOutput output;
if ( ! f->RayCast( &output, input ) )
continue;
if ( output.fraction < closestFraction ) {
closestFraction = output.fraction;
intersectionNormal = output.normal;
}
}
}
b2Vec2 intersectionPoint = p1 + closestFraction * (p2 - p1);
//draw this part of the ray
glBegin(GL_LINES);
glVertex2f( p1.x, p1.y );
glVertex2f( intersectionPoint.x, intersectionPoint.y );
glEnd();
if ( closestFraction == 1 )
return; //ray hit nothing so we can finish here
if ( closestFraction == 0 )
return;
//still some ray left to reflect
b2Vec2 remainingRay = (p2 - intersectionPoint);
b2Vec2 projectedOntoNormal = b2Dot(remainingRay, intersectionNormal) * intersectionNormal;
b2Vec2 nextp2 = p2 - 2 * projectedOntoNormal;
//recurse
drawReflectedRay(intersectionPoint, nextp2);
} |
... and then inside Step() you would just have:
1
2
3
4
5
6
7
| //calculate points of ray
float rayLength = 25;
b2Vec2 p1( 0, 20 ); //center of scene
b2Vec2 p2 = p1 + rayLength * b2Vec2( sinf(currentRayAngle), cosf(currentRayAngle) );
glColor3f(1,1,1); //white
drawReflectedRay(p1, p2); |
