Created: April 22 2014
Inverted pendulum is a fancy term for balancing something like a stick or a pole to keep it vertical, by supporting it only at the bottom. As you probably know if you've tried this, the vertical position is an unstable state and the natural
result is for the stick to accelerate away from it. It can be stabilized with a fast enough
controller, eg. your eye/brain/hand, or a computer, that can react in real-time and move the support point.
As you probably know if you've tried this, the vertical position is an unstable state and the natural
result is for the stick to accelerate away from it. It can be stabilized with a fast enough
controller, eg. your eye/brain/hand, or a computer, that can react in real-time and move the support point.
It seems like PID controllers are commonly used to keep this kind of situation stable. When using one for another project recently I found they are actually extremely simple, so thought I would also try using them for inverted pendulums in Box2D.
I made three variations, the first has the 'cart' on a prismatic joint, which allows for exact (and unrealistic) control by setting the motor speed to whatever is needed. The second two variations are carts on wheels, and are more limited in the control they have because they depend on friction between the wheels and the ground, and the torque of the wheels themselves spinning can interfere a little: A basic controller for a single variable can be written in a few dozen lines of code.
Each time step, you tell it what the current error is, and 'step' it for a specific time length, similar to a Box2D step.
The output value of the controller is then applied to whatever will affect the error - in this case
The controller error is of course the angle deviation from vertical, which is easy to find.
A basic controller for a single variable can be written in a few dozen lines of code.
Each time step, you tell it what the current error is, and 'step' it for a specific time length, similar to a Box2D step.
The output value of the controller is then applied to whatever will affect the error - in this case
The controller error is of course the angle deviation from vertical, which is easy to find.
The target speed here is the speed that the cart should move at. For the first case, this can be set directly
as the motor speed of the prismatic joint. For the other two cases, dividing the speed by the circumference of the
wheels will give the angular velocity that the wheels should turn at, which is given as the motor speed of the wheel joints.
The not-so-simple part of all this is deciding what the 'gain' values should be for the controller. There is a proper way to design these controllers so that they are optimal, and there is a huge amount of info around on the net about that. However the math made my head hurt, so I just played with the numbers for a while until I got a reasonable result. If the required speed exceeds a maximum limit, the controller will give up and do nothing instead of speeding off into the distance.
This simple controller works fairly well to keep the angle of the pendulum vertical, but the cart will usually move away from the position it started at. It should also be noted that the angle of the pendulum corresponds to an acceleration of the cart. For example, to hold the pendulum at a constant angle of 5 degrees the cart would need to accelerate at a constant rate - it would need to continuously get faster and faster. To hold the pendulum at a constant angle of zero means that the acceleration of the cart will be zero. Acceleration of zero means that speed is not changing... but it does not mean that speed is zero. The result of this situation is that when the pendulum stabilizes in a vertical position, the cart will have a constant speed. To stabilize the speed of the cart, or even better bring it to a specific position, another controller is needed.
Since the angle of the pendulum corresponds to an acceleration of the cart, changing the target angle of the pendulum from zero to something else will cause a change of speed of the cart. The question that stumped me for a while was the exact relationship between pendulum angle and cart acceleration. I finally found some math I could understand here (PDF), which points out that the angular acceleration of the pendulum can be written in two ways: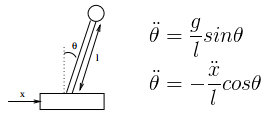 ... where g is gravity. This can be rewritten and solved to find the angle required to produce a given acceleration:
... where g is gravity. This can be rewritten and solved to find the angle required to produce a given acceleration:
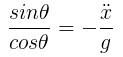 Okay it's not solved, but my head was still hurting from earlier, and I noticed that sin/cos is
basically linear for the part of it that I'm interested in:
Okay it's not solved, but my head was still hurting from earlier, and I noticed that sin/cos is
basically linear for the part of it that I'm interested in:
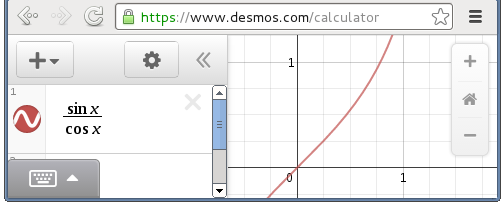 The point of this graph probably seems quite obtuse, but since the other side of the equation is the cart acceleration over gravity,
you could think of the vertical axis as 'g-force' and the horizontal axis is the angle of the pendulum away from vertical.
The graph line shows how much g-force is required to maintain the pendulum constantly at a given angle.
The important thing to see is that as the pendulum angle
increases, the corresponding cart acceleration increases linearly up until about 0.5, which is roughly 30 degrees.
This means the relationship between pendulum angle and cart acceleration can be considered as linear for the
purposes of this little experiment (any angle over 30 degrees is a lost cause anyway).
The point of this graph probably seems quite obtuse, but since the other side of the equation is the cart acceleration over gravity,
you could think of the vertical axis as 'g-force' and the horizontal axis is the angle of the pendulum away from vertical.
The graph line shows how much g-force is required to maintain the pendulum constantly at a given angle.
The important thing to see is that as the pendulum angle
increases, the corresponding cart acceleration increases linearly up until about 0.5, which is roughly 30 degrees.
This means the relationship between pendulum angle and cart acceleration can be considered as linear for the
purposes of this little experiment (any angle over 30 degrees is a lost cause anyway).
(Side note: apparently Formula One cars can accelerate at about 1.4g until about 200km/h, which according to this graph would let them maintain a pendulum at about 55 degrees away from vertical during that time. That must be quite a ride!)
Since I had my PID controller class ready I used a second controller to adjust the desired angle based on the current position of the cart, to make it move left or right. This is probably not the best way but it does ok. The code is similar to above, with input error being the difference between current position and desired position, and the output being a target angle for the pendulum.
Turns out it was not really necessary to bother with the equations above since the controller can do an ok job as long as it's given decent gain settings, but it was nice to know the input and output are linear, and it makes me feel smart to have formula markup and graphs in my blog. In future if I make a more sophisticated controller, eg. maintain a target velocity, that formula could be used as part of a proper calculation for target angle.
Check out these links for some cool related things:
Source code: iforce2d-invertedPendulum-src.zip
Binaries for Win32, Mac, Linux64: iforce2d-invertedPendulum-bin.zip
Inverted pendulum control
Inverted pendulum is a fancy term for balancing something like a stick or a pole to keep it vertical, by supporting it only at the bottom.
 As you probably know if you've tried this, the vertical position is an unstable state and the natural
result is for the stick to accelerate away from it. It can be stabilized with a fast enough
controller, eg. your eye/brain/hand, or a computer, that can react in real-time and move the support point.
As you probably know if you've tried this, the vertical position is an unstable state and the natural
result is for the stick to accelerate away from it. It can be stabilized with a fast enough
controller, eg. your eye/brain/hand, or a computer, that can react in real-time and move the support point.It seems like PID controllers are commonly used to keep this kind of situation stable. When using one for another project recently I found they are actually extremely simple, so thought I would also try using them for inverted pendulums in Box2D.
I made three variations, the first has the 'cart' on a prismatic joint, which allows for exact (and unrealistic) control by setting the motor speed to whatever is needed. The second two variations are carts on wheels, and are more limited in the control they have because they depend on friction between the wheels and the ground, and the torque of the wheels themselves spinning can interfere a little:
 A basic controller for a single variable can be written in a few dozen lines of code.
Each time step, you tell it what the current error is, and 'step' it for a specific time length, similar to a Box2D step.
The output value of the controller is then applied to whatever will affect the error - in this case
The controller error is of course the angle deviation from vertical, which is easy to find.
A basic controller for a single variable can be written in a few dozen lines of code.
Each time step, you tell it what the current error is, and 'step' it for a specific time length, similar to a Box2D step.
The output value of the controller is then applied to whatever will affect the error - in this case
The controller error is of course the angle deviation from vertical, which is easy to find.
1 2 3 | angleController.setError( targetAngle - pendulumBody->GetAngle() ); angleController.step( 1 / 60.0 ); float targetSpeed = angleController.getOutput(); |
The not-so-simple part of all this is deciding what the 'gain' values should be for the controller. There is a proper way to design these controllers so that they are optimal, and there is a huge amount of info around on the net about that. However the math made my head hurt, so I just played with the numbers for a while until I got a reasonable result. If the required speed exceeds a maximum limit, the controller will give up and do nothing instead of speeding off into the distance.
This simple controller works fairly well to keep the angle of the pendulum vertical, but the cart will usually move away from the position it started at. It should also be noted that the angle of the pendulum corresponds to an acceleration of the cart. For example, to hold the pendulum at a constant angle of 5 degrees the cart would need to accelerate at a constant rate - it would need to continuously get faster and faster. To hold the pendulum at a constant angle of zero means that the acceleration of the cart will be zero. Acceleration of zero means that speed is not changing... but it does not mean that speed is zero. The result of this situation is that when the pendulum stabilizes in a vertical position, the cart will have a constant speed. To stabilize the speed of the cart, or even better bring it to a specific position, another controller is needed.
Since the angle of the pendulum corresponds to an acceleration of the cart, changing the target angle of the pendulum from zero to something else will cause a change of speed of the cart. The question that stumped me for a while was the exact relationship between pendulum angle and cart acceleration. I finally found some math I could understand here (PDF), which points out that the angular acceleration of the pendulum can be written in two ways:
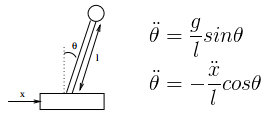 ... where g is gravity. This can be rewritten and solved to find the angle required to produce a given acceleration:
... where g is gravity. This can be rewritten and solved to find the angle required to produce a given acceleration:
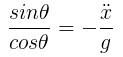 Okay it's not solved, but my head was still hurting from earlier, and I noticed that sin/cos is
basically linear for the part of it that I'm interested in:
Okay it's not solved, but my head was still hurting from earlier, and I noticed that sin/cos is
basically linear for the part of it that I'm interested in:
 The point of this graph probably seems quite obtuse, but since the other side of the equation is the cart acceleration over gravity,
you could think of the vertical axis as 'g-force' and the horizontal axis is the angle of the pendulum away from vertical.
The graph line shows how much g-force is required to maintain the pendulum constantly at a given angle.
The important thing to see is that as the pendulum angle
increases, the corresponding cart acceleration increases linearly up until about 0.5, which is roughly 30 degrees.
This means the relationship between pendulum angle and cart acceleration can be considered as linear for the
purposes of this little experiment (any angle over 30 degrees is a lost cause anyway).
The point of this graph probably seems quite obtuse, but since the other side of the equation is the cart acceleration over gravity,
you could think of the vertical axis as 'g-force' and the horizontal axis is the angle of the pendulum away from vertical.
The graph line shows how much g-force is required to maintain the pendulum constantly at a given angle.
The important thing to see is that as the pendulum angle
increases, the corresponding cart acceleration increases linearly up until about 0.5, which is roughly 30 degrees.
This means the relationship between pendulum angle and cart acceleration can be considered as linear for the
purposes of this little experiment (any angle over 30 degrees is a lost cause anyway).(Side note: apparently Formula One cars can accelerate at about 1.4g until about 200km/h, which according to this graph would let them maintain a pendulum at about 55 degrees away from vertical during that time. That must be quite a ride!)
Since I had my PID controller class ready I used a second controller to adjust the desired angle based on the current position of the cart, to make it move left or right. This is probably not the best way but it does ok. The code is similar to above, with input error being the difference between current position and desired position, and the output being a target angle for the pendulum.
Turns out it was not really necessary to bother with the equations above since the controller can do an ok job as long as it's given decent gain settings, but it was nice to know the input and output are linear, and it makes me feel smart to have formula markup and graphs in my blog. In future if I make a more sophisticated controller, eg. maintain a target velocity, that formula could be used as part of a proper calculation for target angle.
Check out these links for some cool related things:
- Arduino-based balancing robot
- 2-dimensional inverted pendulum horizontal vertical
- Double pendulum!! Triple pendulum!!!
- Solowheel
- Ballbot
- Quadcopters throw and catch inverted pendulum
- Huge rocket hovers and lands (SpaceX Falcon9)
- PID controller and Stewart-Gough platform
Source code: iforce2d-invertedPendulum-src.zip
Binaries for Win32, Mac, Linux64: iforce2d-invertedPendulum-bin.zip